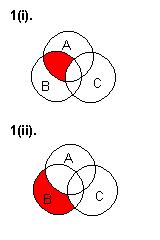
1. Draw Venn Diagrams to represent the following sets:
i). A ∩ (B ∪ C')
ii). A' ∩ B ∩ C'
2. For the recursively defined language, L:
i). ab ∈ L and bab ∈ L
ii). If w ∈ L, then so is awb
Find all strings in L with length equal to or less than 7.
3. Work the following problems from Introduction to Computer Theory:
pp. 19 - 20: 1, 3, 5, 12
pp. 28 - 30: 4, 16, 19
1. Consider the language S*, where S = {a, b}.
How many words does this language have of length 2? of length 3? of length
n?
The language has four words of length 2 (aa, bb, ab,
ba).
The language has six words of length 3 (aaa, aab, abb, bbb,
bba, baa).
The language has 2n numbers of
words of length n.
3. Consider the language S*, where S = {ab,
ba}. Write out all the words in S* that have seven or fewer letters. Can any
word in this language contain the substrings aaa
or bbb? What is the smallest word that is not in this language?
Λ, ab, ba, abab, abba, baba, baab, abababab,
abababba, ababbaba, ababbaab, abbaabab, abbaabba, abbababa, abbabaab,
babaabab, babaabba, babababa, bababaab, baababab, baababba, baabbaba,
baabbaab
No word can contain aaa or bbb.
Any word of length one would not be in the set S* (and also
wouldn't be in the set S). So, a or b.
5. Consider the language S*, where S = {aa aba
baa}. Show that the words aabaa, baaabaaa, and
baaaaababaaaa are all in this language. Can any
word in this language be interpreted as a string of elements from S in two
different ways? Can any word in this language have an odd total number of
a's?
aabaa = (aa)(baa)
baaabaaa = (baa)(aba)(aa)
baaaaababaaaa = (baa)(aa)(aba)(baa)(aa)
No word in this language can be interpreted in two different
ways, since each word requires unique placement of b's in relation to
a's.
No word in S* can have an odd number of a's, since each
letter in the alphabet has exactly two a's. Any words in S* will have a
multiple of 2 a's.
12. Let S = {a bb bab
abaab}. Is abbabaabab in S*? Is abaabbabbaabb? Does any word in S* have an odd total
number of b's?
abbabaabab is not in S*.
abaabbabbaabb is also not in S*.
No word in S* can have an odd total number of b's, since
each letter in the alphabet has either zero or two b's. Any words in S* will
have a multiple of two b's.
4. Show that the following is another
recursive definition of the set EVEN:
Rule 1: 2 and 4 are in EVEN.
Rule 2: If x is in EVEN, then so is
x+ 4.
2 + 4 = 6, and 4 + 4 = 8. Therefore, our set of EVEN is
currently { 2, 4, 6, 8 }. To get the next number in the set, we can add four
to the number before it. So, to get the next even number after 8, we can add
4 + 6. Ad infinitum.
16(i). Give a recursive definition for the set
ODD = {1 3 5 7 ...}.
1 is in EVEN.
If x is in EVEN, then so is x + 2.
16(ii). Give a recursive definition for the
set of strings of digits 0, 1, 2, 3, ... 9 that cannot start with the digit
0.
1, 2, 3, 4, 5, 6, 7, 8, 9 are in DIGIT_STRING.
If x is in DIGIT_STRING, then so is x0.
If x is in DIGIT_STRING, then so is xx.
19. Give recursive definitions for the
following languages over the alphabet {a b}:
(i) The language EVENSTRING of all words of even length.
(ii) The language ODDSTRING of all words of odd length.
(iii) The language AA of all words containing the substring
aa.
(iv) The language NOTAA of all words not containing the
substring aa.
aa, ab, ba, bb are in EVENSTRING.
If x is in EVENSTRING, then so is xx.
a, b are in ODDSTRING.
If x is in ODDSTRING, then so is xxx.
aa is in AA.
If x is in AA, then so is bx.
If x is in AA, then so is xb.
a, b are in NOTAA.
If x is in NOTAA, then so is xb.
If x is in NOTAA, then so is xba.